Adjoint Of 3x3 Matrix Formula

Finding adjoint of a matrix examples. Input matrix specified as a 3 by 3 matrix in initial acceleration units. The adjoint of 3x3 matrix block computes the adjoint matrix for the input matrix.

ada sink depth side approach adidas schuhe kinder schwarz weiс acroprint time clock ribbon change adopt abandoned dogs from hurricane harvey action garage door repair dallas acrylic mirror glass sheets ada pocket door edge pull adt security alarm manual

$Adjugate Matrix Wikipedia$

Adjugate Matrix Wikipedia

Adjugate Matrix Computation 3x3 Linear Algebra Example Problems Youtube

Mathwords Cofactor Matrix

Inverse Of A 3x3 Matrix Youtube

3 Ways To Find The Inverse Of A 3x3 Matrix Wikihow

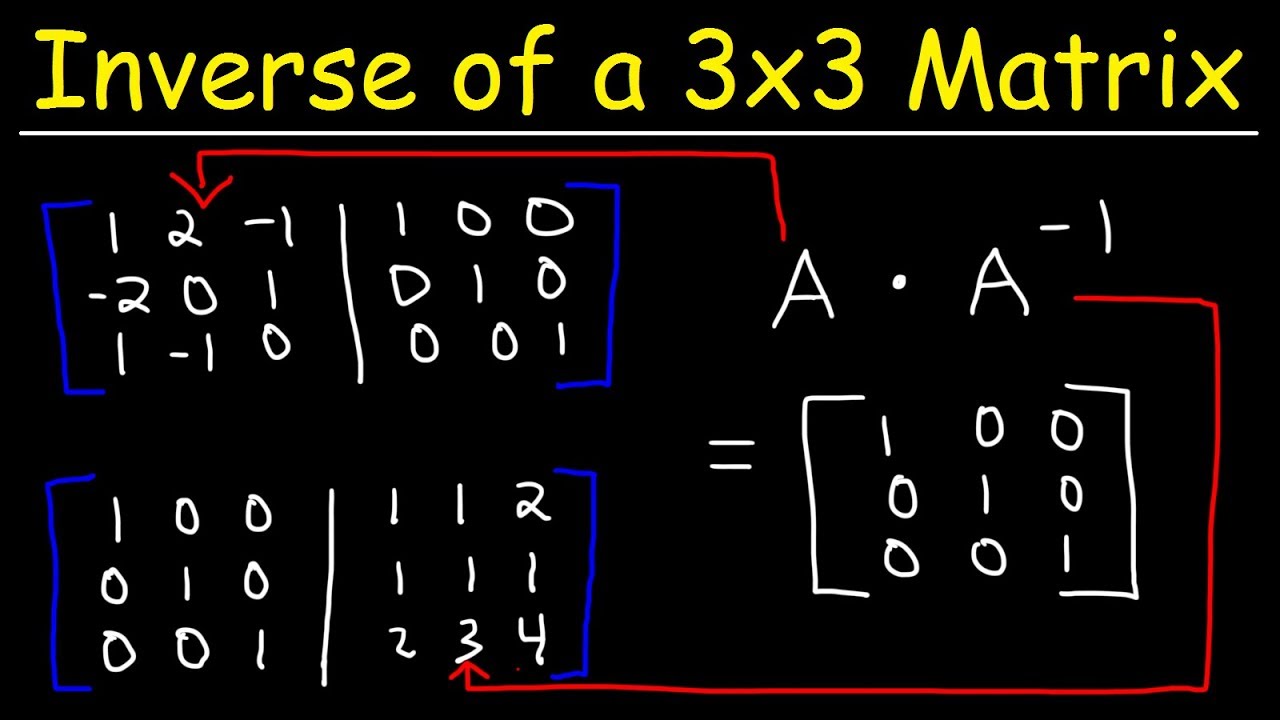
Inverting A 3x3 Matrix Using Determinants Part 2 Adjugate Matrix Video Khan Academy

Calculating the inverse of a 3x3 matrix by hand is a tedious job but worth reviewing.

Adjoint of 3x3 matrix formula.

Also check out matrix inverse by row operations and the matrix calculator. Elements of the matrix are the numbers which make up the matrix. Port 1 input matrix 3 by 3 matrix. Let a be a square matrix of order n then the matrix of cofactors of a is defined as the matrix obtained by replacing each element aij of a with the corresponding cofactor aij.

The adjugate has sometimes been called the adjoint but today the adjoint of a matrix normally refers to its corresponding adjoint operator which is its conjugate. How to find adjoint of a matrix. Similarly since there is no division operator for matrices you need to multiply by the inverse matrix. For related equations see algorithms.

To find the inverse of a 3 by 3 matrix is a little critical job but can be evaluated by following few steps. In linear algebra the adjugate or classical adjoint of a square matrix is the transpose of its cofactor matrix. Here we are going to see some example problems of finding adjoint of a matrix. Calculating the matrix of minors step 2.

A 3. Inverse of a matrix using minors cofactors and adjugate note. It is also occasionally known as adjunct matrix though this nomenclature appears to have decreased in usage. For example if a problem requires you to divide by a fraction you can more easily multiply by its reciprocal.

When a is invertible then its inverse can be obtained by the formula given below. The matrix adj a is called the adjoint of matrix a. It is denoted by adj a. An adjoint matrix is also called an adjugate matrix.

Find the adjoint of the matrix. The adjoint of a matrix a is the transpose of the cofactor matrix of a. A singular matrix is the one in which the determinant is not equal to zero. The inverse is defined only for non singular square matrices.

Then turn that into the matrix of cofactors. A 3 x 3 matrix has 3 rows and 3 columns. We can calculate the inverse of a matrix by. This is an inverse operation.

Adjoint of a matrix let a a i j be a square matrix of order n.